PSF Matching (photutils.psf.matching)

Introduction

This subpackage contains tools to generate kernels for matching point spread functions (PSFs).

Matching PSFs

Photutils provides a function called create_matching_kernel() that generates a matching kernel between two PSFs using the ratio of Fourier transforms (see e.g., Gordon et al. 2008; Aniano et al. 2011).

For this first simple example, let’s assume our source and target PSFs are noiseless 2D Gaussians. The “high-resolution” PSF will be a Gaussian with \(\sigma=3\). The “low-resolution” PSF will be a Gaussian with \(\sigma=5\):

>>> import numpy as np
>>> from astropy.modeling.models import Gaussian2D
>>> y, x = np.mgrid[0:51, 0:51]
>>> gm1 = Gaussian2D(100, 25, 25, 3, 3)
>>> gm2 = Gaussian2D(100, 25, 25, 5, 5)
>>> g1 = gm1(x, y)
>>> g2 = gm2(x, y)
>>> g1 /= g1.sum()
>>> g2 /= g2.sum()

For these 2D Gaussians, the matching kernel should be a 2D Gaussian with \(\sigma=4\) (sqrt(5**2 - 3**2)). Let’s create the matching kernel using a Fourier ratio method. Note that the input source and target PSFs must have the same shape and pixel scale:

>>> from photutils.psf import create_matching_kernel
>>> kernel = create_matching_kernel(g1, g2)

Let’s plot the result:

(Source code, png, hires.png, pdf, svg)

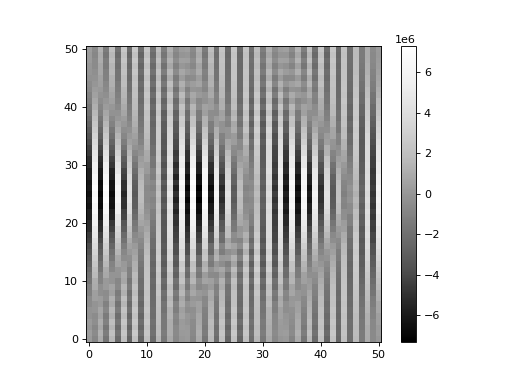
We quickly observe that the result is not as expected. This is because of high-frequency noise in the Fourier transforms (even though these are noiseless PSFs, there is floating-point noise in the ratios). Using the Fourier ratio method, one must filter the high-frequency noise from the Fourier ratios. This is performed by inputting a window function, which may be a function or a callable object. In general, the user will need to exercise some care when defining a window function. For more information, please see Aniano et al. 2011.

Photutils provides the following window classes:

• HanningWindow

• TukeyWindow

• CosineBellWindow

• SplitCosineBellWindow

• TopHatWindow

Here are plots of 1D cuts across the center of the 2D window functions:

(Source code, png, hires.png, pdf, svg)

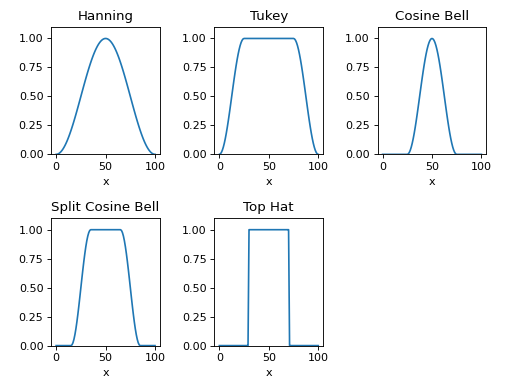
However, the user may input any function or callable object to generate a custom window function.

In this example, because these are noiseless PSFs, we will use a TopHatWindow object as the low-pass filter:

>>> from photutils.psf import TopHatWindow
>>> window = TopHatWindow(0.35)
>>> kernel = create_matching_kernel(g1, g2, window=window)

Note that the output matching kernel from create_matching_kernel() is always normalized such that the kernel array sums to 1:

>>> print(kernel.sum())  
1.0

Let’s display the new matching kernel:

(Source code, png, hires.png, pdf, svg)

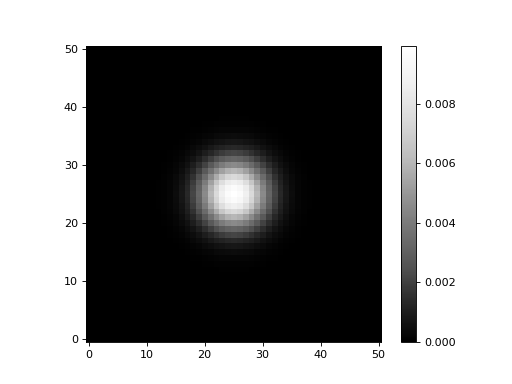
As desired, the result is indeed a 2D Gaussian with a \(\sigma=4\). Here we will show 1D cuts across the center of the kernel images:

(Source code, png, hires.png, pdf, svg)

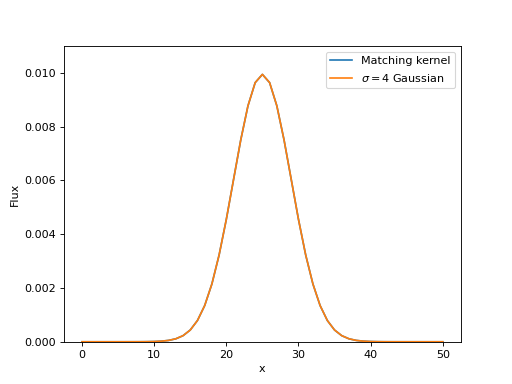
Matching IRAC PSFs

For this example, let’s generate a matching kernel to go from the Spitzer/IRAC channel 1 (3.6 microns) PSF to the channel 4 (8.0 microns) PSF. We load the PSFs using the load_irac_psf() convenience function:

>>> from photutils.datasets import load_irac_psf
>>> ch1_hdu = load_irac_psf(channel=1)  
>>> ch4_hdu = load_irac_psf(channel=4)  
>>> ch1 = ch1_hdu.data  
>>> ch4 = ch4_hdu.data  

Let’s display the images:

(Source code, png, hires.png, pdf, svg)

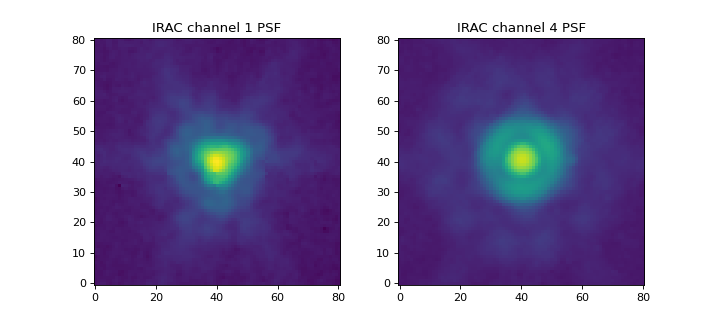
For this example, we will use the CosineBellWindow for the low-pass window. Note that these Spitzer/IRAC channel 1 and 4 PSFs have the same shape and pixel scale. If that is not the case, one can use the resize_psf() convenience function to resize a PSF image. Typically, one would interpolate the lower-resolution PSF to the same size as the higher-resolution PSF.

>>> from photutils.psf import CosineBellWindow, create_matching_kernel
>>> window = CosineBellWindow(alpha=0.35)
>>> kernel = create_matching_kernel(ch1, ch4, window=window)

Let’s display the matching kernel result:

(Source code, png, hires.png, pdf, svg)

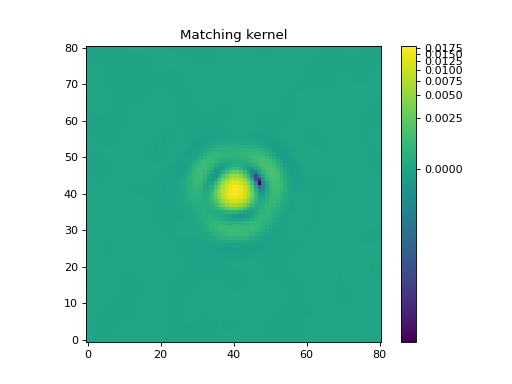
The Spitzer/IRAC channel 1 image could then be convolved with this matching kernel to produce an image with the same resolution as the channel-4 image.

Reference/API

This subpackage contains tools to generate kernels for matching point spread functions.

Functions

create_matching_kernel(source_psf, target_psf, *)	Create a kernel to match 2D point spread functions (PSF) using the ratio of Fourier transforms.
resize_psf(psf, input_pixel_scale, ...[, order])	Resize a PSF using spline interpolation of the requested order.

Classes

CosineBellWindow(alpha)	Class to define a 2D cosine bell window function.
HanningWindow()	Class to define a 2D Hanning (or Hann) window function.
SplitCosineBellWindow(alpha, beta)	Class to define a 2D split cosine bell taper function.
TopHatWindow(beta)	Class to define a 2D top hat window function.
TukeyWindow(alpha)	Class to define a 2D Tukey window function.

Class Inheritance Diagram