Centroids (photutils.centroids)¶
Introduction¶
photutils.centroids provides several functions to calculate the
centroid of a single source:
centroid_com(): Calculates the object “center of mass” from 2D image moments.centroid_quadratic(): Calculates the centroid by fitting a 2D quadratic polynomial to the data.centroid_1dg(): Calculates the centroid by fitting 1D Gaussians to the marginalxandydistributions of the data.centroid_2dg(): Calculates the centroid by fitting a 2D Gaussian to the 2D distribution of the data.
Masks can be input into each of these functions to mask bad pixels. Error arrays can be input into the two Gaussian fitting methods to weight the fits.
To calculate the centroids of many sources in an image, use the
centroid_sources() function. This function
can be used with any of the above centroiding functions or a custom
user-defined centroiding function.
Getting Started¶
Let’s extract a single object from a synthetic dataset and find its centroid with each of these methods. For this simple example we will not subtract the background from the data (but in practice, one should subtract the background):
>>> from photutils.datasets import make_4gaussians_image
>>> from photutils.centroids import (centroid_1dg, centroid_2dg,
... centroid_com, centroid_quadratic)
>>> data = make_4gaussians_image()[43:79, 76:104]
>>> x1, y1 = centroid_com(data)
>>> print((x1, y1))
(13.93157998341213, 17.051234441067088)
>>> x2, y2 = centroid_quadratic(data)
>>> print((x2, y2))
(13.948284438186919, 16.98788199435759)
>>> x3, y3 = centroid_1dg(data)
>>> print((x3, y3))
(14.040352707371396, 16.962306463644801)
>>> x4, y4 = centroid_2dg(data)
>>> print((x4, y4))
(14.002212073733611, 16.996134592982017)
Now let’s plot the results. Because the centroids are all very similar, we also include an inset plot zoomed in near the centroid:
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import (mark_inset,
zoomed_inset_axes)
from photutils.centroids import (centroid_1dg, centroid_2dg,
centroid_com, centroid_quadratic)
from photutils.datasets import make_4gaussians_image
data = make_4gaussians_image()[43:79, 76:104] # extract single object
xycen1 = centroid_com(data)
xycen2 = centroid_quadratic(data)
xycen3 = centroid_1dg(data)
xycen4 = centroid_2dg(data)
xycens = [xycen1, xycen2, xycen3, xycen4]
fig, ax = plt.subplots(1, 1, figsize=(4, 5))
ax.imshow(data, origin='lower', interpolation='nearest')
marker = '+'
ms, mew = 15, 2.0
colors = ('white', 'black', 'red', 'blue')
for xycen, color in zip(xycens, colors):
plt.plot(*xycen, color=color, marker=marker, ms=ms, mew=mew)
ax2 = zoomed_inset_axes(ax, zoom=6, loc=9)
ax2.imshow(data, vmin=190, vmax=220, origin='lower',
interpolation='nearest')
ms, mew = 30, 2.0
for xycen, color in zip(xycens, colors):
ax2.plot(*xycen, color=color, marker=marker, ms=ms, mew=mew)
ax2.set_xlim(13, 15)
ax2.set_ylim(16, 18)
mark_inset(ax, ax2, loc1=3, loc2=4, fc='none', ec='0.5')
ax2.axes.get_xaxis().set_visible(False)
ax2.axes.get_yaxis().set_visible(False)
ax.set_xlim(0, data.shape[1] - 1)
ax.set_ylim(0, data.shape[0] - 1)
(Source code, png, hires.png, pdf, svg)
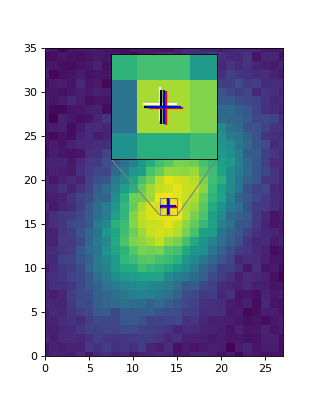
Centroiding several sources in an image¶
The centroid_sources() function can be used
to calculate the centroids of many sources in a single image given
initial guesses for their positions. This function can be used with any
of the above centroiding functions or a custom user-defined centroiding
function.
Here is a simple example using
centroid_com(). A cutout image is made
centered at each initial position of size box_size. A centroid is
then calculated within the cutout image for each source:
>>> from photutils.centroids import centroid_sources
>>> data = make_4gaussians_image()
>>> x_init = (25, 91, 151, 160)
>>> y_init = (40, 61, 24, 71)
>>> x, y = centroid_sources(data, x_init, y_init, box_size=21,
... centroid_func=centroid_com)
>>> print(x)
[ 24.98911515 90.43056554 150.20332399 159.87234831]
>>> print(y)
[40.08504359 60.56869612 24.74216925 70.32723054]
Let’s plot the results:
import matplotlib.pyplot as plt
from photutils.centroids import centroid_com, centroid_sources
from photutils.datasets import make_4gaussians_image
data = make_4gaussians_image()
x_init = (25, 91, 151, 160)
y_init = (40, 61, 24, 71)
x, y = centroid_sources(data, x_init, y_init, box_size=21,
centroid_func=centroid_com)
plt.figure(figsize=(8, 4))
plt.imshow(data, origin='lower', interpolation='nearest')
plt.scatter(x, y, marker='+', s=80, color='red', label='Centroids')
plt.legend()
plt.tight_layout()
(Source code, png, hires.png, pdf, svg)
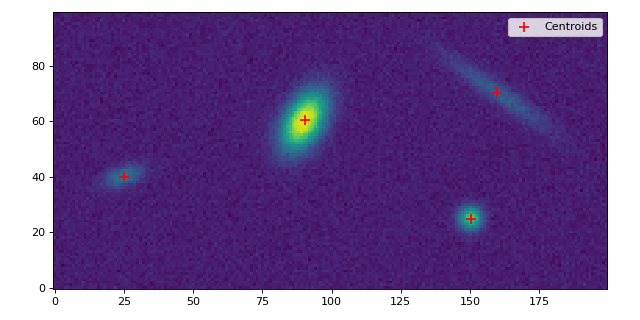
Reference/API¶
This subpackage contains tools for centroiding sources.
Functions¶
|
Calculate the centroid of a 2D array by fitting 1D Gaussians to the marginal |
|
Calculate the centroid of a 2D array by fitting a 2D Gaussian (plus a constant) to the array. |
|
Calculate the centroid of an n-dimensional array as its "center of mass" determined from moments. |
|
Calculate the centroid of an n-dimensional array by fitting a 2D quadratic polynomial. |
|
Calculate the centroid of sources at the defined positions. |