Aperture Photometry (photutils.aperture)¶
Introduction¶
The aperture_photometry() function and the
ApertureStats class are the main tools to
perform aperture photometry on an astronomical image for a given set of
apertures.
Photutils provides several apertures defined in pixel or sky coordinates. The aperture classes that are defined in pixel coordinates are:
Each of these classes has a corresponding variant defined in sky coordinates:
To perform aperture photometry with sky-based apertures, one will need to specify a WCS transformation.
Users can also create their own custom apertures (see Defining Your Own Custom Apertures).
Creating Aperture Objects¶
The first step in performing aperture photometry is to create an aperture object. An aperture object is defined by a position (or a list of positions) and parameters that define its size and possibly, orientation (e.g., an elliptical aperture).
We start with an example of creating a circular aperture in pixel
coordinates using the CircularAperture
class:
>>> from photutils.aperture import CircularAperture
>>> positions = [(30.0, 30.0), (40.0, 40.0)]
>>> aperture = CircularAperture(positions, r=3.0)
The positions should be either a single tuple of (x, y), a list of
(x, y) tuples, or an array with shape Nx2, where N is the
number of positions. The above example defines two circular apertures
located at pixel coordinates (30, 30) and (40, 40) with a
radius of 3 pixels.
Creating an aperture object in sky coordinates is similar. One first
uses the SkyCoord class to define sky
coordinates and then the
SkyCircularAperture class to define the
aperture object:
>>> from astropy import units as u
>>> from astropy.coordinates import SkyCoord
>>> from photutils.aperture import SkyCircularAperture
>>> positions = SkyCoord(l=[1.2, 2.3] * u.deg, b=[0.1, 0.2] * u.deg,
... frame='galactic')
>>> aperture = SkyCircularAperture(positions, r=4.0 * u.arcsec)
Note
Sky apertures are not defined completely in sky coordinates. They simply use sky coordinates to define the central position, and the remaining parameters are converted to pixels using the pixel scale of the image at the central position. Projection distortions are not taken into account. They are not defined as apertures on the celestial sphere, but rather are meant to represent aperture shapes on an image. If the apertures were defined completely in sky coordinates, their shapes would not be preserved when converting to or from pixel coordinates.
Converting Between Pixel and Sky Apertures¶
The pixel apertures can be converted to sky apertures, and
vice versa, given a WCS object. To accomplish this, use the
to_sky() method for pixel
apertures, e.g.,:
>>> aperture = CircularAperture((10, 20), r=4.0)
>>> sky_aperture = aperture.to_sky(wcs)
and the to_pixel() method for
sky apertures, e.g.,:
>>> position = SkyCoord(1.2, 0.1, unit='deg', frame='icrs')
>>> aperture = SkyCircularAperture(position, r=4.0 * u.arcsec)
>>> pix_aperture = aperture.to_pixel(wcs)
Performing Aperture Photometry¶
After the aperture object is created, we can then perform the photometry
using the aperture_photometry() function. We
start by defining the aperture (at two positions) as described above:
>>> positions = [(30.0, 30.0), (40.0, 40.0)]
>>> aperture = CircularAperture(positions, r=3.0)
We then call the aperture_photometry()
function with the data and the apertures. Note that
aperture_photometry() assumes that the input
data have been background subtracted. For simplicity, we define the data
here as an array of all ones:
>>> import numpy as np
>>> from photutils.aperture import aperture_photometry
>>> data = np.ones((100, 100))
>>> phot_table = aperture_photometry(data, aperture)
>>> phot_table['aperture_sum'].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum
pix pix
--- ------- ------- ------------
1 30.0 30.0 28.274334
2 40.0 40.0 28.274334
This function returns the results of the photometry in an Astropy
QTable. In this example, the table has four columns,
named 'id', 'xcenter', 'ycenter', and 'aperture_sum'.
Since all the data values are 1.0, the aperture sums are equal to the area of a circle with a radius of 3:
>>> print(np.pi * 3.0 ** 2)
28.2743338823
Aperture and Pixel Overlap¶
The overlap of the aperture with the data pixels can be handled in
different ways. The default method (method='exact') calculates the
exact intersection of the aperture with each pixel. The
other options, 'center' and 'subpixel', are faster, but with
the expense of less precision. With 'center', a pixel is
considered to be entirely in or out of the aperture depending on
whether its center is in or out of the aperture. With 'subpixel',
pixels are divided into a number of subpixels, which are in or out of
the aperture based on their centers. For this method, the number of
subpixels needs to be set with the subpixels keyword.
This example uses the 'subpixel' method where pixels are resampled
by a factor of 5 (subpixels=5) in each dimension:
>>> phot_table = aperture_photometry(data, aperture, method='subpixel',
... subpixels=5)
>>> print(phot_table)
id xcenter ycenter aperture_sum
pix pix
--- ------- ------- ------------
1 30.0 30.0 27.96
2 40.0 40.0 27.96
Note that the results differ from the exact value of 28.274333 (see above).
For the 'subpixel' method, the default value is subpixels=5,
meaning that each pixel is equally divided into 25 smaller pixels
(this is the method and subsampling factor used in SourceExtractor).
The precision can be increased by increasing subpixels, but note
that computation time will be increased.
Aperture Photometry with Multiple Apertures at Each Position¶
While the Aperture objects support multiple
positions, they must have a fixed size and shape (e.g., radius and
orientation).
To perform photometry in multiple apertures at each position, one may
input a list of aperture objects to the
aperture_photometry() function. In this
case, the apertures must all have identical position(s).
Suppose that we wish to use three circular apertures, with radii of 3, 4, and 5 pixels, on each source:
>>> radii = [3.0, 4.0, 5.0]
>>> apertures = [CircularAperture(positions, r=r) for r in radii]
>>> phot_table = aperture_photometry(data, apertures)
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum_0 aperture_sum_1 aperture_sum_2
pix pix
--- ------- ------- -------------- -------------- --------------
1 30 30 28.274334 50.265482 78.539816
2 40 40 28.274334 50.265482 78.539816
For multiple apertures, the output table column names are appended
with the positions index.
Other apertures have multiple parameters specifying the aperture size
and orientation. For example, for elliptical apertures, one must
specify a, b, and theta:
>>> from astropy.coordinates import Angle
>>> from photutils.aperture import EllipticalAperture
>>> a = 5.0
>>> b = 3.0
>>> theta = Angle(45, 'deg')
>>> apertures = EllipticalAperture(positions, a, b, theta)
>>> phot_table = aperture_photometry(data, apertures)
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum
pix pix
--- ------- ------- ------------
1 30 30 47.12389
2 40 40 47.12389
Again, for multiple apertures one should input a list of aperture objects, each with identical positions:
>>> a = [5.0, 6.0, 7.0]
>>> b = [3.0, 4.0, 5.0]
>>> theta = Angle(45, 'deg')
>>> apertures = [EllipticalAperture(positions, a=ai, b=bi, theta=theta)
... for (ai, bi) in zip(a, b)]
>>> phot_table = aperture_photometry(data, apertures)
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum_0 aperture_sum_1 aperture_sum_2
pix pix
--- ------- ------- -------------- -------------- --------------
1 30 30 47.12389 75.398224 109.95574
2 40 40 47.12389 75.398224 109.95574
Aperture Statistics¶
The ApertureStats class can be
used to create a catalog of statistics and properties for
pixels within an aperture, including aperture photometry.
It can calculate many properties, including statistics
like min,
max,
mean,
median,
std,
sum_aper_area,
and sum. It
also can be used to calculate morphological properties
like centroid,
fwhm,
semimajor_sigma,
semiminor_sigma,
orientation, and
eccentricity. Please see
ApertureStats for the complete
list of properties that can be calculated. The properties can be
accessed using ApertureStats attributes
or output to an Astropy QTable using the
to_table() method.
Most of the source properties are calculated using the “center”
aperture-mask method, which gives
aperture weights of 0 or 1. This avoids the need to compute weighted
statistics — the data pixel values are directly used.
The sum_method and subpixels keywords are used to determine
the aperture-mask method when calculating the sum-related properties:
sum, sum_error, sum_aper_area, data_sumcutout, and
error_sumcutout. The default is sum_method='exact', which
produces exact aperture-weighted photometry.
The optional local_bkg keyword can be used to input the per-pixel
local background of each source, which will be subtracted before
computing the aperture statistics.
The optional sigma_clip keyword can be used to sigma clip the pixel
values before computing the source properties. This keyword could be
used, for example, to compute a sigma-clipped median of pixels in an
annulus aperture to estimate the local background level.
Here is a simple example using a circular aperture at one position.
Note that like aperture_photometry(),
ApertureStats expects the input data to
be background subtracted. For simplicity, here we roughly estimate the
background as the sigma-clipped median value:
>>> from astropy.stats import sigma_clipped_stats
>>> from photutils.aperture import ApertureStats, CircularAperture
>>> from photutils.datasets import make_4gaussians_image
>>> data = make_4gaussians_image()
>>> _, median, _ = sigma_clipped_stats(data, sigma=3.0)
>>> data -= median # subtract background from the data
>>> aper = CircularAperture((150, 25), 8)
>>> aperstats = ApertureStats(data, aper)
>>> print(aperstats.xcentroid)
149.98572304129868
>>> print(aperstats.ycentroid)
24.996938431105146
>>> print(aperstats.centroid)
[149.98572304 24.99693843]
>>> print(aperstats.mean, aperstats.median, aperstats.std)
41.45359513219223 28.335251716057705 38.25291812758177
>>> print(aperstats.sum)
8030.736512250234
Similar to aperture_photometry, the input aperture
can have multiple positions:
>>> aper2 = CircularAperture(((150, 25), (90, 60)), 10)
>>> aperstats2 = ApertureStats(data, aper2)
>>> print(aperstats2.xcentroid)
[149.96671384 90.00873475]
>>> print(aperstats2.sum)
[ 8164.51010709 34930.47721039]
>>> columns = ('id', 'mean', 'median', 'std', 'var', 'sum')
>>> stats_table = aperstats2.to_table(columns)
>>> for col in stats_table.colnames:
... stats_table[col].info.format = '%.8g' # for consistent table output
>>> print(stats_table)
id mean median std var sum
--- --------- --------- --------- --------- ---------
1 26.792685 11.13497 36.189318 1309.6667 8164.5101
2 113.09856 111.77054 50.10054 2510.0641 34930.477
Each row of the table corresponds to a single aperture position (i.e., a single source).
Background Subtraction¶
Global Background Subtraction¶
aperture_photometry() and
ApertureStats assume that the input data
have been background-subtracted. If bkg is a float value or an
array representing the background of the data (e.g., determined by
Background2D or an external function), simply
subtract the background from the data:
>>> phot_table = aperture_photometry(data - bkg, aperture)
In the case of a constant global background, you can pass in the background
value using local_bkg in ApertureStats.
This would avoid reading an entire memory-mapped array into memory
beforehand, as would happen if you manually subtract the background as
shown above. So instead you could do this:
>>> aperstats = ApertureStats(data, aperture, local_bkg=bkg)
Local Background Subtraction¶
One often wants to also estimate the local background around
each source using a nearby aperture or annulus aperture
surrounding each source. A simple method for doing this is to
use the ApertureStats class (see
Aperture Statistics) to compute the mean background level
within the background aperture. This class can also be used to calculate
more advanced statistics (e.g., a sigma-clipped median) within the
background aperture (e.g., a circular annulus). We show examples of both
below.
Let’s start by generating a more realistic example dataset:
>>> from photutils.datasets import make_100gaussians_image
>>> data = make_100gaussians_image()
This artificial image has a known constant background level of 5. In the following examples, we’ll leave this global background in the image to be estimated using local backgrounds.
For this example we perform the photometry for three sources in a circular aperture with a radius of 5 pixels. The local background level around each source is estimated using a circular annulus of inner radius 10 pixels and outer radius 15 pixels. Let’s define the apertures:
>>> from photutils.aperture import CircularAnnulus, CircularAperture
>>> positions = [(145.1, 168.3), (84.5, 224.1), (48.3, 200.3)]
>>> aperture = CircularAperture(positions, r=5)
>>> annulus_aperture = CircularAnnulus(positions, r_in=10, r_out=15)
Now let’s plot the circular apertures (white) and circular annulus apertures (red) on a cutout from the image containing the three sources:
(Source code, png, hires.png, pdf, svg)
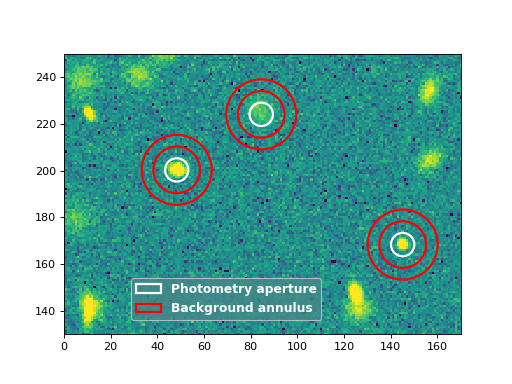
Simple mean within a circular annulus¶
We can use the ApertureStats class to
compute the mean background level within the annulus aperture at each
position:
>>> from photutils.aperture import ApertureStats
>>> aperstats = ApertureStats(data, annulus_aperture)
>>> bkg_mean = aperstats.mean
>>> print(bkg_mean)
[4.96369499 5.10467691 4.9497741 ]
Now let’s use aperture_photometry() to perform
the photometry in the circular aperture (in the next example, we’ll use
ApertureStats to perform the photometry):
>>> from photutils.aperture import aperture_photometry
>>> phot_table = aperture_photometry(data, aperture)
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum
pix pix
--- ------- ------- ------------
1 145.1 168.3 1131.5794
2 84.5 224.1 746.16064
3 48.3 200.3 1250.2186
The total background within the circular aperture is the mean local
per-pixel background times the circular aperture area. If you are
using the default “exact” aperture (see aperture-mask methods) and there are no masked pixels, the exact
analytical aperture area can be accessed via the aperture area
attribute:
>>> aperture.area
78.53981633974483
However, in general you should use the
photutils.aperture.PixelAperture.area_overlap() method where
a mask keyword can be input. This ensures you are using the
same area over which the photometry was performed. If using a
SkyAperture, you will first need to convert
it to a PixelAperture. Since we are not
using a mask, the results are identical:
>>> aperture_area = aperture.area_overlap(data)
>>> print(aperture_area)
[78.53981634 78.53981634 78.53981634]
The total background within the circular aperture is then:
>>> total_bkg = bkg_mean * aperture_area
>>> print(total_bkg)
[389.84769319 400.92038721 388.75434843]
Thus, the background-subtracted photometry is:
>>> phot_bkgsub = phot_table['aperture_sum'] - total_bkg
Finally, let’s add these as columns to the photometry table:
>>> phot_table['total_bkg'] = total_bkg
>>> phot_table['aperture_sum_bkgsub'] = phot_bkgsub
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum total_bkg aperture_sum_bkgsub
pix pix
--- ------- ------- ------------ --------- -------------------
1 145.1 168.3 1131.5794 389.84769 741.73173
2 84.5 224.1 746.16064 400.92039 345.24026
3 48.3 200.3 1250.2186 388.75435 861.46422
Sigma-clipped median within a circular annulus¶
For this example, the local background level around each source is
estimated as the sigma-clipped median value within the circular annulus.
We’ll use the ApertureStats class to
compute both the photometry (aperture sum) and the background level:
>>> from astropy.stats import SigmaClip
>>> sigclip = SigmaClip(sigma=3.0, maxiters=10)
>>> aper_stats = ApertureStats(data, aperture, sigma_clip=None)
>>> bkg_stats = ApertureStats(data, annulus_aperture, sigma_clip=sigclip)
The sigma-clipped median values in the background annulus apertures are:
>>> print(bkg_stats.median)
[4.848213 5.0884354 4.80605993]
The total background within the circular apertures is then the per-pixel background level multiplied by the circular-aperture areas:
>>> total_bkg = bkg_stats.median * aper_stats.sum_aper_area.value
>>> print(total_bkg)
[380.77775843 399.64478152 377.46706442]
Finally, the local background-subtracted sum within the circular apertures is:
>>> apersum_bkgsub = aper_stats.sum - total_bkg
>>> print(apersum_bkgsub)
[750.80166351 346.51586233 872.75150158]
Note that if you want to compute all the source properties (i.e., in
addition to only sum) on the
local-background-subtracted data, you may input the per-pixel local
background values to ApertureStats via the
local_bkg keyword:
>>> aper_stats_bkgsub = ApertureStats(data, aperture,
... local_bkg=bkg_stats.median)
>>> print(aper_stats_bkgsub.sum)
[750.80166351 346.51586233 872.75150158]
Note these background-subtracted values are the same as those above.
Aperture Photometry Error Estimation¶
If and only if the error keyword is input to
aperture_photometry(), the returned table
will include a 'aperture_sum_err' column in addition to
'aperture_sum'. 'aperture_sum_err' provides the propagated
uncertainty associated with 'aperture_sum'.
For example, suppose we have previously calculated the error on each
pixel value and saved it in the array error:
>>> positions = [(30.0, 30.0), (40.0, 40.0)]
>>> aperture = CircularAperture(positions, r=3.0)
>>> data = np.ones((100, 100))
>>> error = 0.1 * data
>>> phot_table = aperture_photometry(data, aperture, error=error)
>>> for col in phot_table.colnames:
... phot_table[col].info.format = '%.8g' # for consistent table output
>>> print(phot_table)
id xcenter ycenter aperture_sum aperture_sum_err
pix pix
--- ------- ------- ------------ ----------------
1 30 30 28.274334 0.53173616
2 40 40 28.274334 0.53173616
'aperture_sum_err' values are given by:
\[\Delta F = \sqrt{\sum_{i \in A} \sigma_{\mathrm{tot}, i}^2}\]
where \(A\) are the non-masked pixels in the aperture, and
\(\sigma_{\mathrm{tot}, i}\) is the input error array.
In the example above, it is assumed that the error keyword
specifies the total error — either it includes Poisson noise
due to individual sources or such noise is irrelevant. However, it
is often the case that one has calculated a smooth “background-only
error” array, which by design doesn’t include increased noise on bright
pixels. To include Poisson noise from the sources, we can use the
calc_total_error() function.
Let’s assume we have a background-only image called bkg_error.
If our data are in units of electrons/s, we would use the exposure
time as the effective gain:
>>> from photutils.utils import calc_total_error
>>> effective_gain = 500 # seconds
>>> error = calc_total_error(data, bkg_error, effective_gain)
>>> phot_table = aperture_photometry(data - bkg, aperture, error=error)
Aperture Photometry with Pixel Masking¶
Pixels can be ignored/excluded (e.g., bad pixels) from the aperture
photometry by providing an image mask via the mask keyword:
>>> data = np.ones((5, 5))
>>> aperture = CircularAperture((2, 2), 2.0)
>>> mask = np.zeros(data.shape, dtype=bool)
>>> data[2, 2] = 100.0 # bad pixel
>>> mask[2, 2] = True
>>> t1 = aperture_photometry(data, aperture, mask=mask)
>>> t1['aperture_sum'].info.format = '%.8g' # for consistent table output
>>> print(t1['aperture_sum'])
aperture_sum
------------
11.566371
The result is very different if a mask image is not provided:
>>> t2 = aperture_photometry(data, aperture)
>>> t2['aperture_sum'].info.format = '%.8g' # for consistent table output
>>> print(t2['aperture_sum'])
aperture_sum
------------
111.56637
Aperture Photometry Using Sky Coordinates¶
As mentioned in Creating Aperture Objects, performing
photometry using apertures defined in sky coordinates simply requires
defining a “sky” aperture at positions defined by a
SkyCoord object. Here we show an
example of photometry on real data using a
SkyCircularAperture.
We start by loading a Spitzer 4.5 micron image of a region of the Galactic plane:
>>> import astropy.units as u
>>> from astropy.wcs import WCS
>>> from photutils.datasets import load_spitzer_catalog, load_spitzer_image
>>> hdu = load_spitzer_image()
>>> data = u.Quantity(hdu.data, unit=hdu.header['BUNIT'])
>>> wcs = WCS(hdu.header)
>>> catalog = load_spitzer_catalog()
The catalog contains (among other things) the Galactic coordinates of the sources in the image as well as the PSF-fitted fluxes from the official Spitzer data reduction. We define the apertures positions based on the existing catalog positions:
>>> positions = SkyCoord(catalog['l'], catalog['b'], frame='galactic')
>>> aperture = SkyCircularAperture(positions, r=4.8 * u.arcsec)
Now perform the photometry in these apertures on the data. The
wcs object contains the WCS transformation of the image obtained
from the FITS header. It includes the coordinate frame of the image
and the projection from sky to pixel coordinates. The
aperture_photometry function uses the WCS
information to automatically convert the apertures defined in sky
coordinates into pixel coordinates:
>>> phot_table = aperture_photometry(data, aperture, wcs=wcs)
The Spitzer catalog also contains the official fluxes for the sources, so we can compare to our fluxes. Because the Spitzer catalog fluxes are in units of mJy and the data are in units of MJy/sr, we need to convert units before comparing the results. The image data have a pixel scale of 1.2 arcsec/pixel.
>>> import astropy.units as u
>>> factor = (1.2 * u.arcsec) ** 2 / u.pixel
>>> fluxes_catalog = catalog['f4_5']
>>> converted_aperture_sum = (phot_table['aperture_sum'] *
... factor).to(u.mJy / u.pixel)
Finally, we can plot the comparison of the photometry:
>>> import matplotlib.pyplot as plt
>>> plt.scatter(fluxes_catalog, converted_aperture_sum.value)
>>> plt.xlabel('Spitzer catalog PSF-fit fluxes ')
>>> plt.ylabel('Aperture photometry fluxes')
(Source code, png, hires.png, pdf, svg)
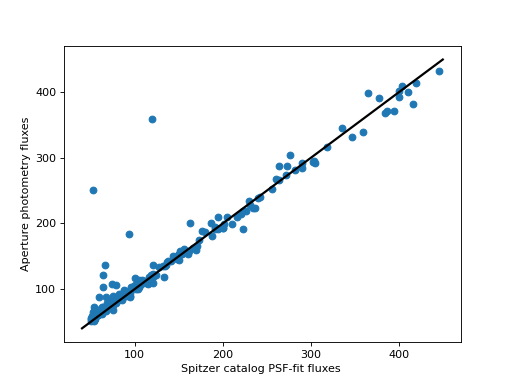
Despite using different methods, the two catalogs are in good agreement. The aperture photometry fluxes are based on a circular aperture with a radius of 4.8 arcsec. The Spitzer catalog fluxes were computed using PSF photometry. Therefore, differences are expected between the two measurements.
Aperture Masks¶
All PixelAperture objects have a
to_mask() method that returns
a ApertureMask object (for a single aperture
position) or a list of ApertureMask objects, one
for each aperture position. The ApertureMask
object contains a cutout of the aperture mask weights and a
BoundingBox object that provides the bounding box
where the mask is to be applied.
Let’s start by creating a circular-annulus aperture:
>>> from photutils.aperture import CircularAnnulus
>>> from photutils.datasets import make_100gaussians_image
>>> data = make_100gaussians_image()
>>> positions = [(145.1, 168.3), (84.5, 224.1), (48.3, 200.3)]
>>> aperture = CircularAnnulus(positions, r_in=10, r_out=15)
Now let’s create a list of ApertureMask objects
using the to_mask() method using
the aperture mask “exact” method:
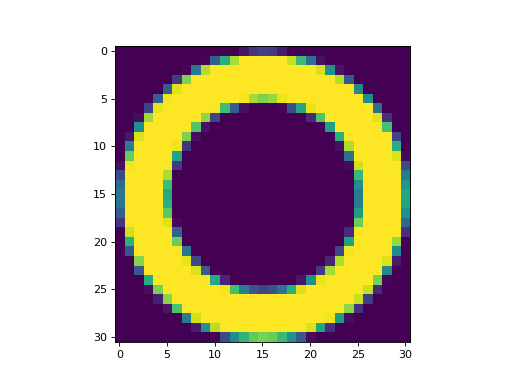
>>> masks = aperture.to_mask(method='exact')
Let’s plot the first aperture mask:
>>> import matplotlib.pyplot as plt
>>> plt.imshow(masks[0])
(Source code, png, hires.png, pdf, svg)
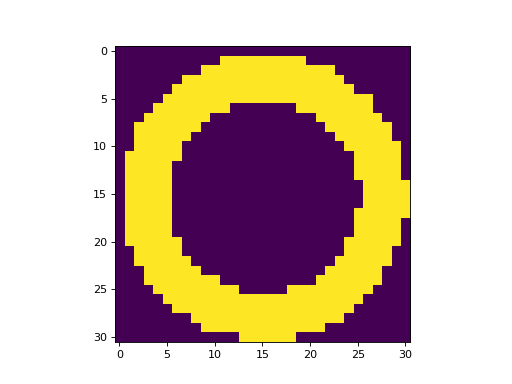
Let’s now use the “center” aperture mask method and plot the resulting aperture mask:
>>> masks2 = aperture.to_mask(method='center')
>>> plt.imshow(masks2[0])
(Source code, png, hires.png, pdf, svg)
We can also create an aperture mask-weighted cutout from the data, properly handling the cases of partial or no overlap of the aperture mask with the data. Let’s plot the aperture mask weights (using the mask generated above with the “exact” method) multiplied with the data:
>>> data_weighted = masks[0].multiply(data)
>>> plt.imshow(data_weighted)
(Source code, png, hires.png, pdf, svg)
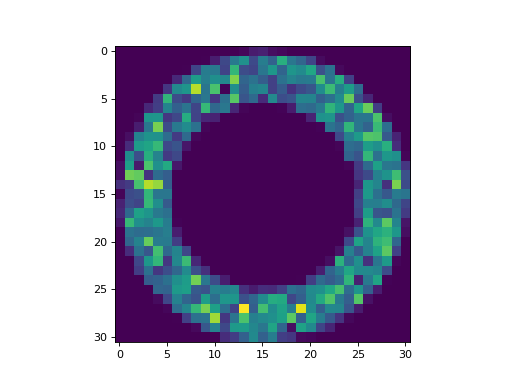
To get a 1D ndarray of the non-zero weighted data values, use
the get_values() method:
>>> data_weighted_1d = masks[0].get_values(data)
The ApertureMask class also provides a
to_image() method to obtain
an image of the aperture mask in a 2D array of the given shape and a
cutout() method to create a
cutout from the input data over the aperture mask bounding box. Both of
these methods properly handle the cases of partial or no overlap of the
aperture mask with the data.
Defining Your Own Custom Apertures¶
The aperture_photometry() function can
perform aperture photometry in arbitrary apertures. This function
accepts any Aperture-derived objects, such as
CircularAperture. This makes it simple to
extend functionality: a new type of aperture photometry simply
requires the definition of a new Aperture
subclass.
All PixelAperture subclasses must define a
bounding_boxes property and to_mask() and plot() methods.
They may also optionally define an area property. All
SkyAperture subclasses must only implement a
to_pixel() method.
bounding_boxes: The minimal bounding box for the aperture. If the aperture is scalar, then a singleBoundingBoxis returned. Otherwise, a list ofBoundingBoxis returned.
area: An optional property defining the exact analytical area (in pixels**2) of the aperture.
to_mask(): Return a mask for the aperture. If the aperture is scalar, then a singleApertureMaskis returned. Otherwise, a list ofApertureMaskis returned.
plot(): A method to plot the aperture on amatplotlib.axes.Axesinstance.
Reference/API¶
This subpackage contains tools to perform aperture photometry.
Functions¶
|
Perform aperture photometry on the input data by summing the flux within the given aperture(s). |
Classes¶
|
Abstract base class for all apertures. |
|
Class for an aperture mask. |
|
Class to create a catalog of statistics for pixels within an aperture. |
|
A rectangular bounding box in integer (not float) pixel indices. |
|
A circular annulus aperture defined in pixel coordinates. |
|
A circular aperture defined in pixel coordinates. |
Mixin class to create masks for circular and circular-annulus aperture objects. |
|
|
An elliptical annulus aperture defined in pixel coordinates. |
|
An elliptical aperture defined in pixel coordinates. |
Mixin class to create masks for elliptical and elliptical-annulus aperture objects. |
|
Abstract base class for apertures defined in pixel coordinates. |
|
|
A rectangular annulus aperture defined in pixel coordinates. |
|
A rectangular aperture defined in pixel coordinates. |
Mixin class to create masks for rectangular or rectangular-annulus aperture objects. |
|
Abstract base class for all apertures defined in celestial coordinates. |
|
|
A circular annulus aperture defined in sky coordinates. |
|
A circular aperture defined in sky coordinates. |
|
An elliptical annulus aperture defined in sky coordinates. |
|
An elliptical aperture defined in sky coordinates. |
|
A rectangular annulus aperture defined in sky coordinates. |
|
A rectangular aperture defined in sky coordinates. |